Auteur : Thierry Ciblac_
DOI : https://doi.org/10.48568/dkdx-c991
[Après deux articles sur les blobs et metaballs, abordant leur cristallisation dans l’imaginaire des architectes des 90’s, voici une présentation de ces mêmes objets du point de vue géométrique. Objectif du présent papier : comprendre le fonctionnement des metaballs pour les programmer, ici en VB sur Grasshopper (le code est en ligne).]
Nous allons ici illustrer la notion de fonction de potentiel permettant de définir des surfaces implicites. Sera utilisée une fonction de potentiel à rayon d’action limité inspirée de celle présentée par Triquet et al. (1999). On se donne un nombre n de points dans l’espace que l’on nomme primitives. Ces points seront appelés Pi, i étant un indice variant de 1 à n. Ces points Pi peuvent être imaginés comme appartenant à un squelette que l’on voudrait habiller de matière. Le rayon d’action Ri de chaque point permettra de définir jusqu’où il est possible d’ajouter de la matière autour du squelette. Pour chaque primitive on peut définir une fonction potentielle qui définira un champ scalaire dans l’espace calculé en fonction du rayon d’action. Dans notre exemple cette fonction prend des valeurs positives décroissantes jusqu’à devenir nulles au delà du rayon d’influence. C’est-à-dire qu’en tout point de l’espace on associera un nombre qui sera maximal en Pi et nul sur la sphère centrée en Pi de rayon Ri et au-delà.
Comment cela se traduit-il mathématiquement dans notre exemple ?
Les points Pi ont comme coordonnées (xi,yi,zi).
Pour tout point P(x,y,z), on calcule la distance di entre P et Pi.
di2 = (x – xi)2 + (y – yi) 2 + (z – zi) 2
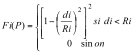 Pour définir le potentiel créé par toutes les primitives, classiquement on additionne les Fi :
Pour définir le potentiel créé par toutes les primitives, classiquement on additionne les Fi :
![]() Avec cette expression on peut calculer en chaque point P de l’espace la valeur du potentiel F et chercher l’ensemble des points pour lesquels F>0, F>constante ou F=constante (par exemple F=0.323).
Avec cette expression on peut calculer en chaque point P de l’espace la valeur du potentiel F et chercher l’ensemble des points pour lesquels F>0, F>constante ou F=constante (par exemple F=0.323).
Si on considère l’ensemble des points vérifiant F>0, on conservera tous les points de potentiels non nuls car par définition de la fonction on a toujours F≥0. L’ensemble de ces points sera de nature volumique tout comme l’ensemble plus restreint formé par l’ensemble des points vérifiant F≥k où k est une constante >0. Augmenter k revient à faire « maigrir » le volume si bien qu’à partir d’une certaine valeur, il ne reste plus rien !
L’ensemble de points vérifiant F=k est lui de nature surfacique, ce qui permet de n’envisager que la peau du volume défini par F≥k.
L’expression F=k est alors l’écriture condensée de l’équation d’une surface implicite.
Une stratégie pour aborder le problème en informatique consiste à découper l’espace en petits cubes dans une zone définie et d’évaluer la fonction potentielle en aux sommets de ces cubes puis ne de conserver que les points vérifiant la condition choisie sur F. Cette méthode présente l’inconvénient d’être coûteuse en temps de calcul si on explore tous les points de la zone prédéfinie, on peut l’améliorer en se limitant aux zones d’influence des primitives.
Nous utilisons cette méthode dans l’application sur Grasshopper. Dans cette application, on définit deux constantes nommées potentiel et incrément afin de n’afficher que les points vérifiant la double inégalité :
potentiel ≥ F ≥ potentiel +incrément
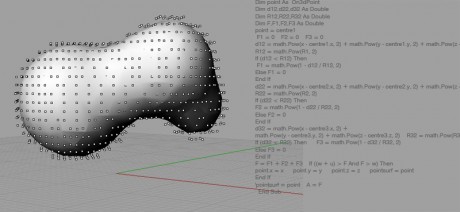
La figure ci-dessous présente un nuage de points dans le cas de trois primitives.
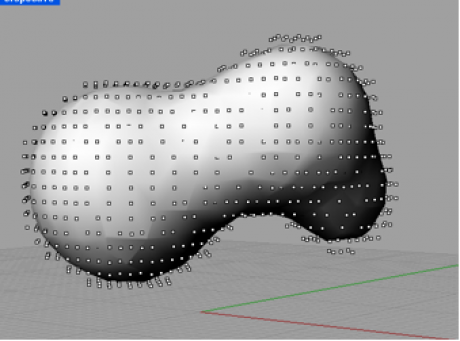
La figure suivante montre une surface construite à partir des points trouvés à l’aide de la fonction « maillage à partir de points » de Rhinoceros.
Pour citer cet article
Thierry Ciblac « Surfaces implicites et fonction de potentiel », DNArchi, 29,/02/12, <http://dnarchi.fr/boiteoutils/surfaces-implicites-et-fonction-de-potentiel>
Codes à télécharger
Script Grasshopper : 2012-02_TC_srf-implicites-3-centres.ghx
Grasshopper definition pour v0.8.0006
Support Rhinoceros 4 : tc/2012-02_TC_srf-implicites-3-centres.3dm
Références bibliographiques
Frédéric Triquet, Philippe Meseure et Christophe Chaillou, « Affichage interactif de surfaces implicites », Actes des Rencontres de l’Association Française d’Informatique Graphique (AFIG), 1999 [en ligne], URL: <http://www-lil.univ-littoral.fr/~renaud/AFIG/RENCONTRES/ACTES/ACTES99/LIFL_Triquet.pdf>