Auteur : Louis Vitalis_

2/3 — La conception dans le calcul

[Nous avons précédemment décrit le rôle joué par une équation dans le processus de conception du parc de la Villette de Rem Koolhaas (1/3 Un calcul dans la conception).]

On peut penser que cette première approche de l’équation restait encore externe à l’équation elle-même. Si elle éclaire son contexte d’origine et les opérations qu’elle laisse ensuite à la discrétion des concepteurs pour terminer le travail, elle n’explicite que ce qu’il y a, en quelque sorte, « autour » du calcul. Il peut sembler que cette action de produire un résultat qui n’existait pas auparavant (« f ») en se basant sur des variables connues ait quelque rapport avec la conception. Or, énoncer cela revient à brouiller la distinction entre concevoir et calculer , et mérite donc quelques précisions.

Si l’on considère l’équation elle-même au titre d’une supposée conception, une difficulté apparaît. Il semble que les variables « A », « a » et « x » forment ce par rapport à quoi le résultat est calculé. Elles joueraient alors le rôle de « références ». Cela conduit à se demander s’il faut tenir compte aussi, en plus de la référence issue du discours de l’architecte, des références issues de l’équation pour comprendre la conception. Mais ces variables sont-elles des « références » au même titre que les utilisateurs dont on perd la trace dans l’équation ?

Il est possible d’envisager une alternative, toute fictionnelle qu’elle soit[1], qui semble corroborer cette hypothèse d’une conception propre au calcul. L’équation utilisée par l’OMA (appelons là l’équation 1) n’est pas l’unique façon de calculer une fréquence qui soit conforme aux références et pertinences posées par les concepteurs. Voici une alternative possible (appelons là l’équation 2) :

f = v/t

Où, « v » est la vitesse de marche des utilisateurs et « t » un temps considéré comme optimal pour accéder à un service programmatique donné. La différence entre les deux équations signifie-t-elle un rôle du calcul numérique propre à la conception ?

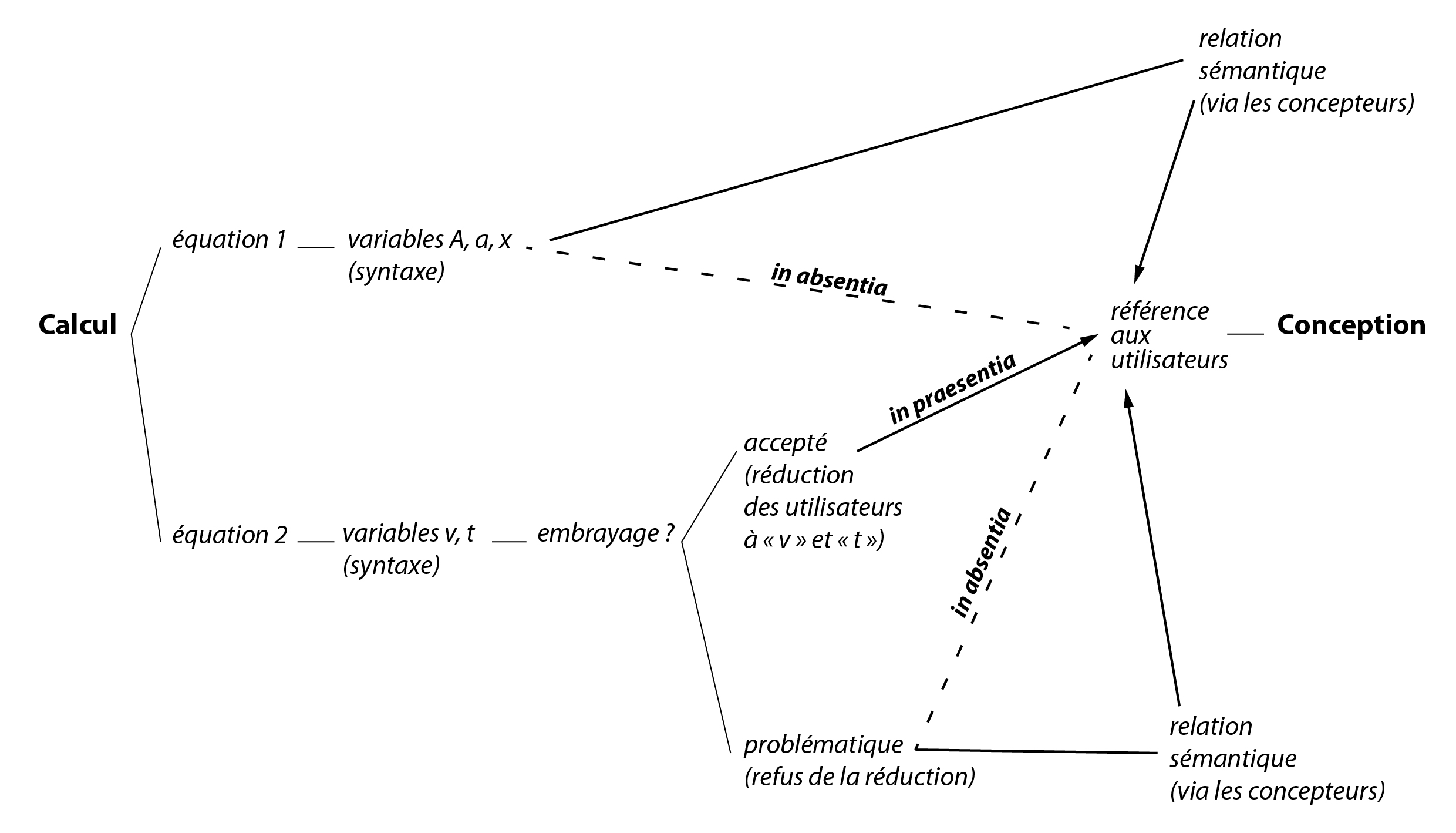
Les deux équations permettent de calculer un « f », du point de vue du calcul il n’y a pas de différence dans la nature du résultat. C’est la manière de le produire qui en revanche diffère. L’équation 2 semble convoquer les utilisateurs au niveau de ses variables « v » et « t ». Les variables n’incarnent pas, bien entendu, les utilisateurs dans leur totalité, mais représentent une partie, un aspect numérique, qui leur est propre. L’équation 1, si l’on s’en tient strictement aux variables ne renvoie elle aucunement aux utilisateurs : « a » et « A » sont déjà des entités spatiales, et « x » une quantité d’éléments programmatiques. Du point de vue de la conception cependant, les utilisateurs sont associés aux deux manières de calculer. La distinction pourrait à 1^ère vue s’exprimer ainsi : l’équation 1 est dans une relation in absentia aux utilisateurs, on pourra qualifier cet aspect de sémantique (ou métaphorique), tandis que l’équation 2 semble être dans une relation in praesentia aux utilisateurs, donc syntaxique (ou métonymique)[2].

Faut-il comprendre que l’équation 2 relève de la conception plus que l’équation 1 ? On peut remarquer que le terme d’accessibilité possède déjà — avant qu’une équation quelconque en fasse une traduction instrumentale — ce double sens. L’accessibilité renvoi d’un côté à un aspect qualitatif, une signification (« c’est accessible ») donc sémantique. Et d’un autre côté, l’accessibilité renvoie à un aspect de contiguïté spatiale, d’ordre alors aussi quantitatif (« l’accès est à telle distance depuis tel endroit »), donc syntaxique ou métonymique.

Lorsque l’on tente de se placer au niveau de l’équation pourtant ces considérations concernant la relation variable/« références » disparaissent puisque l’on se situe dans un espace qui doit être distingué de l’espace de la conception, un espace qu’on pourrait dire géométrique. La fréquence « f » est une variable indépendante au sens où elle résulte d’un choix d’entité à déterminer, un choix de conception. Mais dans l’espace géométrique, ce choix n’a plus de sens et « f », « A », « a », « x », « v » et « t » sont des variables liées. Le fait d’opter pour l’équation 1 ou 2, ne fait pas disparaître les variables de l’autre. Si l’on calcule un « f » à partir de l’équation 1, les variables « v » et « t » pourront toujours être retrouvées (sous forme d’un ensemble de solution) puisqu’elles sont liées métonymiquement dans l’espace géométrique. Du point de vue de la conception « A », « a », « x », « v » et « t » sont des « dimensions » résiduelles de l’espace : ce ne sont pas elles que l’on choisit de déterminer, elles résultent par liaison syntaxique du choix fait.

Pour autant, il semble que les deux équations puissent apparaître différentes aux yeux d’un concepteur. Utiliser l’équation 2 signifiera donner une (ou plusieurs[3]) valeur(s) aux variables « v » et « t » et donc de décider de la vitesse des utilisateurs et d’un temps optimal pour atteindre un type de programme. On comprend alors que les deux séries de variables, « A », « a », « x » et « v », « t », n’ont pas tout à fait le même sens du point de vue d’un choix à faire. Les variables de l’équation 1 ont une valeur qui ne prête pas à discussion, tandis que celles de l’équation 2 présentent une certaine ambigüité : la vitesse d’un utilisateur ne sera pas nécessairement la même d’après Rem Koolhaas, ou un de ces collaborateurs, d’après un flâneur, un riverain pressé, un enfant ou une vieille dame… Il est vraisemblable que certains concepteurs se refusent à figer ce genre de phénomènes fluctuants et donc à déterminer les valeurs de ces variables et préfèrent alors opter pour l’équation 1[4]. Le problème qui se pose est celui de « l’embrayage » (qui signifie l’articulation du modèle avec le réel en architecturologie[5]), considérer l’équation 2 comme embrayante suppose une certaine vision du réel acceptant de représenter les utilisateurs par « v » et « t ». Si cette vision est refusée, l’équation sera perçue comme non-embrayante. Tandis qu’il n’y a pas de raison de considérer l’équation 1 comme non-embrayante puisque l’absence explicite des utilisateurs la rend d’usage non-problématique.

Cette possible réticence vis-à-vis de l’équation 2 amène à reconsidérer la relation de ses variables à la référence des utilisateurs. Le refus de considérer que « v » et « t » puissent incarner les utilisateurs, en tant qu’il est un refus de la réduction d’un utilisateur à sa vitesse et à son temps de parcours, montre que l’articulation au réel est considéré malgré tout comme arbitraire. Les variables de l’équation 2 sont donc aussi dans une relation in absentia aux utilisateurs, ou du moins à ce qui fait la « pertinence » des utilisateurs dans ce cas de conception[6]. Le fait que l’équation 2 puisse renvoyer aux utilisateurs tient alors à un caractère sémantique et ressort donc de l’espace de conception, de même que pour l’équation 1. La différence intuitive d’un degré de proximité entre variables et référence des deux équations résiderait peut-être du côté de la distinction symbolique/indiciel ; l’équation 1 serait symboliquement (rapport arbitraire) en relation avec la référence tandis que l’équation 2 le serait indiciellement (rapport physique), mais toutes deux in absentia.

Cette distinction entre espace géométrique et espace de conception signifie que l’équation ne donne qu’une syntaxe . C’est le concepteur qui en l’utilisant lui confère une sémantique. Observer les relais sémantique>syntaxique et les « embrayages » perçus devrait permettre de modéliser la complexité de la conception architecturale en tant qu’elle met en rapport l’espace géométrique avec des espaces de références qui lui sont hétérogènes.

Constater ainsi une absence d’un niveau sémantique propre au calcul et un espace géométrique procédant de références seulement métonymiques permettrait de conclure par extension à une absence de « pertinence » propre à l’équation pour la conception architecturale. Ce qui signifie aussi la nécessité d’un point de vue sur l’outil numérique . On peut faire l’hypothèse que cette absence de pertinence propre a quelque chose à voir avec la réutilisation des outils de calcul à des fins différentes. On a pu en effet observer la diffusion de « samples » dans la conception paramétrique, qui, choisis dans des librairies de modèles, signifient pour les concepteurs qui les utilisent de « dimensionner un modèle conçu par un autre »[7]. C’est-à-dire très précisément de donner de la pertinence à l’outil. Au-delà des outils numériques, s’observent également des détournements[8] ou plus généralement des catachrèses[9].

En conclusion, nous maintiendrons la distinction entre concevoir et calculer en disant que l’esprit conçoit alors que l’outil ne fait que générer. La pensée utilise cette propriété générative de l’outil pour concevoir. Si la production d’une valeur « f » par l’équation, laisse penser à de la conception c’est parce que ce « f », en tant que distance entre les programmes, n’est pas connu au départ. Pourtant il faut bien voir que « f » en soit n’est rien sans la pensée qui lui attribue la valeur sémantique de « fréquence des programmes », et ainsi la valeur d’« inconnue au départ » ne procède que cette décision. Décision que l’on attribue à la conception.

Suite de l’article ici.

——————————————————————————————————

[1] Nous ne savons pas en l’état de nos données si les concepteurs ont effectivement considéré cette alternative.

[2] Nous tenons à remercier Philippe Boudon de nous avoir indiqué l’utilité de la distinction linguistique in praesentia/in absentia issue de Saussure et Jakobson sur ce point. Elle se trouve détaillée dans Philippe Boudon et al., Enseigner la conception architecturale, op. cit., p. 112.

[3] Dans le cas où l’équation serait utilisée plusieurs fois. On ne rentre pas dans l’amont et l’aval d’un processus dans lequel serait utilisée l’équation 2 et qui bien entendu serait partiellement modifié.

[4] Nous ne prétendons pas que ce soit le cas de Koolhaas (qui au fond nous intéresse moins ici que les conclusions que l’on peut tirer, en général, sur l’utilisation d’équations en conception).

[5] Jean-Louis Le Moigne, « La complexité de la correspondance du modèle au réel : “L’échelle, cette correction capitale” », in Philippe Boudon (dir.), De l’architecture à l’épistémologie. La question de l’échelle, Paris, PUF, 1991, p. 227–248.

[6]  C’est bien le sens d’une pertinence d’ordre fonctionnelle, celui de faire intervenir un « élément externe  » Philippe Boudon, Richelieu, ville nouvelle. Essai d’architecturologie, Paris, Dunod, 1978, p. 12.

[7] Aurélie de Boissieu, « Modélisation paramétrique en conception architecturale : Caractérisation des opérations cognitives de conception pour une pédagogie » ENSA – La Villette / Université Paris Est, thèse sous la direction de François GUENA et Caroline LECOURTOIS, Paris, 2013, p. 243–253.

[8] Églantine Bigot-Doll, Bricologie et Matérialité., http://dnarchi.fr/culture/bricologie-et-materialite/, consulté le 27 mai 2017.

[9] Pierre Rabardel, Les hommes & les technologies. Approche cognitive des instruments contemporains, Paris, Armand Colin, 1995.