Auteur: François Guéna _
DOI : https://doi.org/10.48568/d8dd-3280
RhinoScript est un outil de programmation du modeleur surfacique Rhinoceros. Ce langage permet de développer des programmes en vue d’ajouter de nouvelles fonctionnalités à Rhinoceros ou d’automatiser des tâches répétitives. Il s’agit d’un langage de type Visual Basic Script disposant d’une interface de programmation dans l’application Rhinoceros.
L’interface de programmation d’une application, généralement nommée une API [1] dans le jargon des informaticiens, est une bibliothèque de procédures ou de fonctions qui permet de manipuler les objets d’une application. L’API de Rhinoceros pour RhinoScript est constituée d’un ensemble de méthodes d’un unique objet nommé Rhino. Par l’intermédiaire de ces méthodes, un programme RhinoScript peut créer des objets géométriques (Courbes, Surfaces, etc.), interroger les propriétés de ces éléments (coordonnées de l’origine et de l’extrémité d’une courbe, coordonnées des sommets d’une surface, etc.), leur faire subir des transformations géométriques (translation, rotation, homothétie, etc.) et encore beaucoup d’autres choses. En fait, les méthodes de l’API permettent de manipuler la plupart des éléments de Rhinoceros. Cependant il peut être utile de savoir compléter cette interface de programmation par l’ajout de nouveaux objets et nouvelles méthodes en vue de simplifier les programmes Rhinoscript ou d’accéder à d’autres API.
Pour étendre l’interface de programmation de RhinoScript, le principe consiste à créer des bibliothèques supplémentaires. Une fois ces bibliothèques installées comme des modules externes (Plugins) dans Rhino, un programme RhinoScript peut accéder à l’ensemble des méthodes qu’elles définissent.
Pour créer une nouvelle bibliothèque il faut utiliser un des langages de programmation permettant un accès au SDK[2] de Rhino, à savoir C++, VB.NET ou C# (cf. Grasshopper et la programmation sur Rhinoceros 4: une introduction). Pour utiliser ces langages, il est nécessaire d’avoir reçu une formation en développement informatique.
McNeel met à disposition pour les développeurs des supports expliquant comment créer une API en RhinoScript : en C++ et en VB.NET et C#
Une API externe pour étendre la manipulation des surfaces dans Rhinoscript
Nous mettons à la disposition à la communauté de DNArchi une API, développée en C++, destinée à faciliter la manipulation des surfaces et des solides dans des programmes RhinoScript.
Télécharger l’API ici: 2012-03_FG_Brep.rhp
Brep est le nom de cette API en référence à la technique de représentation des objets par leurs frontières [3] utilisée par Rhino. Elle met à disposition des programmeurs RhinoScript les méthodes permettant de parcourir les sommets, les arêtes et les faces d’un objet Brep et de calculer des coordonnées de points situés sur ces éléments.
Brep.VerticesCount(brepObject) retourne le nombre de sommets,
Brep.EdgesCount(brepObject) retourne le nombre d’arêtes,
Brep.FacesCount(brepObject) retourne le nombre de faces,
Brep.VertexCoordinates(brepObject, index) retourne les coordonnées du ième sommet,
Brep.VerticesCoordinates(brepObject)retourne les coordonnées de tous les sommets,
Brep.EdgePointAtParam(brepObject, index, param) retourne les coordonnées du point de paramètre param sur la ième arête,
Brep.FacePointAtParam(brepObject,index, Uparam, Vparam) retourne les coordonnées d’un point de paramètres Uparam et Vparam sur la ième face
Brep.EdgeMirrorPoint(brepObject, index, point) retourne les coordonnées d’un point orthogonalement symétrique d’un autre par rapport à la ième arête.
Pour pouvoir appeler ces fonctions dans un programme RhinoScript il est nécessaire d’installer le plugin 2012-03_FG_Brep.rhp comme module externe de Rhino 4 [4] (Utiliser le menu Outils/Options/Modules puis installer). Puis dans le programme RhinoScript il faut référencer ce module externe à l’aide de la méthode GetPlugInObject(« nom_du_module_externe »)de l’objet Rhino.
L’instruction Set Brep = Rhino.GetPlugInObject(« Brep ») construit un objet Brep à partir duquel les méthodes de l’API externe seront accessibles.
Pour illustrer l’utilisation de cette bibliothèque, prenons l’exemple de programmes capables de générer des formes à l’aide de grammaires génératives.
La génération de formes à l’aide de grammaires génératives
Une grammaire générative est constituée d’un ensemble de règles de substitution qui analysent une scène et la transforme. Les transformations consistent à remplacer des formes repérées dans la scène par d’autres. Une règle de substitution comporte une partie gauche, exprimant les conditions d’activation de la règle et une partie droite qui décrit la substitution à effectuer. Décrire les conditions d’activation et les substitutions nécessite d’interroger la géométrie des éléments susceptibles de constituer la scène. Les méthodes de la bibliothèque Brep peuvent être utilisées à cette fin.
Le programme qui exploite une grammaire générative est fondé sur un algorithme très simple. Il parcourt l’ensemble des règles de la grammaire, repère celles qui sont activables, active les substitutions puis réitère le processus un nombre de fois donnée. Les grammaires de formes, mais aussi la génération d’objets fractals ou de pavages sont basées sur cette technique algorithmique.
La suite de l’article présente quelques exemples de programmes implémentant des grammaires génératives et utilisant l’API Brep: le tapis et l’éponge de Sierpinski, un pavage de Penrose, et une grammaire de forme en 3D. Tous ces programmes comportent une procédure principale main qui sélectionne les éléments de la scène et active les règles de la grammaire. À chaque règle correspond un sous-programme particulier.
Les partitions de Sierpinsky et de Menger
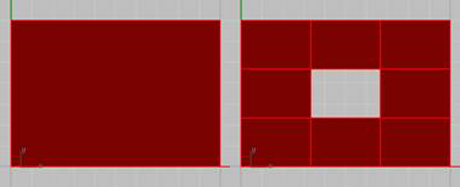
Waclaw Sierpinsky et Karl Menger sont des mathématiciens connus pour leurs travaux réalisés au début du 20ème siècle sur les objets fractals. Le « tapis de Sierpinski » peut être construit en appliquant, à une surface rectangulaire, 4 homothéties de rapport 1/3 centrées sur les sommets du rectangle puis 4 autres homothéties de rapport 1/3 centrées sur le milieu des côtés (cf. Figure 1).
Figure 1 : « Tapis de Sierpinski », application des 8 homothéties au premier niveau
On peut généraliser ce programme pour qu’il s’applique aussi à des solides. On applique une homothétie de rapport 1/3 centrée sur tous les sommets de la forme et sur les milieux des toutes les arêtes.
Les objets fractals de la figure 2 sont produits par les programmes 2012-03_FG_tapis-sierpinski.rvb et 2012-03_FG_eponge-menger.rvb. Comme vous pourrez le voir dans les codes, les deux programmes sont quasiment identiques. Les seules différences portent sur le calcul des couleurs des matériaux utilisées dans le rendu.
Figure 2 : Le « tapis de Sierpinski » et l’ »éponge de Menger »
Un pavage de Penrose
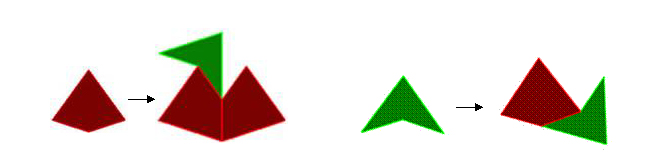
Roger Penrose est un mathématicien et physicien britannique qui découvrit, dans les années 70, un mécanisme de pavage non périodique du plan. Un des pavages de Penrose utilise deux formes de base : le cerf-volant (en rouge ci-dessous) et la fléchette (en vert ci-dessous) [5]. Il s’obtient par l’application de deux règles de substitution présentées dans la figure ci-dessous.
Figure 3 : Les deux règles de substitution du pavage de Penrose «Kite-dart»
Le programme penrose-kite-dart.rvb est développé sur la même structure algorithmique que les précédents. Les deux règles utilisent les méthodes de la bibliothèque Brep pour décrire les transformations. Par exemple pour la première règle, les coordonnées de pp1, pp2 et pp3 sont placées dans un rapport harmonique sur les arêtes 2 et 1 et sur le segment de droite p0p2. Le point pp4 est le point symétrique du point pp3 par rapport à l’arête 2 (cf. Figure 4). À partir des coordonnées de ces points, la règle construit les deux cerfs-volants et la fléchette.
Figure 4 : La transformation d’un cerf-volant en deux cerfs-volants et une fléchette
On procède de manière similaire pour décrire la deuxième règle qui transforme une fléchette en un cerf-volant et une fléchette.
La vidéo ci-dessous présente l’état initial de la scène comportant cinq cerfs-volants (exemple sur Rhino4 à télécharger ici), puis les différents états après chacune des applications des règles de substitution.
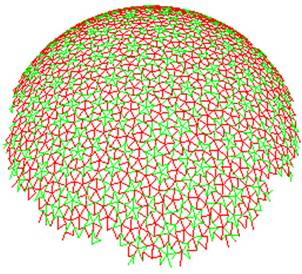
Les pavages de Penrose sont des objets 2D mais on peut les projeter sur différentes surfaces comme le montre la figure 6 ci-dessous.
Figure 6: La projection du pavage Kite-dart sur une sphère.
Une grammaire de forme en 3D
Georges Stiny, professeur au MIT, a développé dans les années 70 le concept de grammaire de formes par analogie avec les grammaires de Chomsky. Une grammaire de formes est constituée d’un vocabulaire de forme primitive et de règles de substitution qui décrivent des catégories de compositions possibles de ces formes. À partir de quelques règles, il est possible de générer des architectures complexes. Le programme grammaire.rvb est développé sur la même base algorithmique que les précédents. La grammaire comprend les deux règles de substitutions présentées ci-dessous. À droite on trouve la forme produite après une vingtaine d’applications de cette grammaire générative.
Figure 7 : Un exemple de grammaire de formes 3D
Les codes à télécharger:
2012-03_FG_penrose-kite-dart.rvb
2012-03_FG_tapis-sierpinski.rvb
Pour citer cet article
François Guéna, « Etendre l’interface de programmation de RhinoScript », DNArchi, 15/03/2012, <http://dnarchi.fr/boiteoutils/etendre-linterface-de-programmation-de-rhinoscript/>
Notes :
[1] Application Programming Interface
[2] SDK : System Development Kit
[3] Brep : Abréviation de Boundary Representation . Il s’agit d’une technique de représentation des objets en 3D par leurs frontières. Dans un modèle Brep, un objet est représenté pas les surfaces qui le limitent (ses frontières). Les surfaces sont délimitées par des arêtes qui se rencontrent sur des sommets. Deux surfaces connexes ont une arête commune. Cette technique de représentation est utilisée par la plupart des modeleurs 3D actuels.
[4] La bibliothèque Brep.rhp, actuellement disponible, a été développée autour du SDK de Rhino 4 et ne fonctionne donc que pour cette version de Rhinoceros.
[5] L’encyclopédie des pavages présente les règles de substitution de différents pavages, dont le pavage kirt-dart (cerf-volant et flechette) http://tilings.math.uni-bielefeld.de/substitution_rules/penrose_kite_dart
Références
Noam Chomsky, « Aspects de la théorie syntaxique », Seuil, 1971.
George Stiny, « Shape: Talking about Seeing and Doing », The Mit Press, April 2006.
George Stiny and James Gips, « Algorithmic Aesthetics: Computer Models for Criticism and Design in the Arts », University of California Press, 1978. (version pdf téléchargeable gratuitement sur http://www.
http://wiki.mcneel.com/developer/sdksamples/getpluginobjectinterface
http://wiki.mcneel.com/developer/sdksamples/extendrhinoscript
