M comme Metaballs

Auteur: Anne-Sophie Delaveau_

DOI : https://doi.org/10.48568/xwja-ns36

[Il est des mots qui cristallisent des pans entiers de la culture geeko-architecturale… Devenus tartes à la crème ou surannés, dans notre « abécédaire du numérique » nous mènerons notre enquête sémantique !]

Aujourd’hui, en suite logique du Blob, les « Metaballs » !

valerialaura sous licence NY by CC 2.0

Si l’on demande à un 3D-man à quoi renvoie le terme metaballs, il y a de fortes chances qu’il vous réponde qu’il s’agit à la fois d’une technique d’infographie et des objets conçus grâce à celle-ci. Mais qui sait que derrière ce terme se cache la théorie des surfaces implicites ?

Comme tout objet géométrique, une surface peut être décrite de deux manières différentes : une formulation explicite donne accès explicitement aux coordonnées de chaque point appartenant à cette surface, tandis qu’une formulation implicite donne une relation entre les coordonnées vérifiée en tout point de la surface. Il faut donc mieux parler de formulation explicite ou implicite d’une surface plutôt que de surface explicite ou implicite.

Dans le cas d’une formulation explicite, on peut faire intervenir un maillage polygonal, des coordonnées semi polaires, ou encore un modèle paramétrique pour décrire la surface. L’exemple suivant présente une surface située dans un espace à 3 dimensions, régie par deux paramètres, u et v. Cette surface paramétrique est décrite par 3 équations, dont la formulation permet de connaître facilement (= donne explicitement) chaque coordonnée d’un point appartenant à cette surface :

Dans le cas d’une formulation implicite, on aura affaire à une équation du type f(x, y, z) = 0. Par exemple, une sphère S de centre C (a, b, c) et de rayon R s’écrit ainsi :

> Il est important de noter qu’un même objet géométrique peut être exprimé de diverses manières, le tout étant de choisir la formulation la plus pertinente par rapport à ce que l’on souhaite calculer.

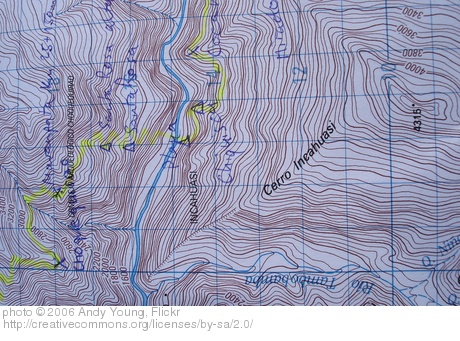
Les connaissances construites dont je viens de donner un aperçu ont fait l’objet de nombreuses applications, en géométrie et en physique notamment. Une application géométrique concerne les champs scalaires qui associent une quantité scalaire (un nombre réel) à tout point de l’espace. On retrouve ce type de champ en physique sous le nom de surface équipotentielle, où la valeur associée au point correspond à son énergie potentielle. Par exemple, sur une carte IGN, chaque courbe de niveau unit les points ayant la même valeur, qui correspond dans ce cas à l’altitude ; l’une courbe de niveaux définit une courbe équipotentielle.

Notre 3D-man en sait désormais un peu plus sur les surfaces implicites décrites implicitement… mais la question « qu’en est-il des metaballs ? » plane toujours!

Jusqu’à présent, nous nous sommes focalisés sur la description des surfaces, non sur leur interaction. Ce qui fait l’intérêt des metaballs pour le 3D-man c’est justement leur capacité à interagir : en créant dans un modeleur 3D deux metaballs et en faisant varier quelques paramètres, une surface joignant les objets est automatiquement générée, comme le montre la vidéo ci-dessous.

Pour générer cette jonction entre les metaballs, le modeleur utilise la formulation implicite de chacun de ces objets géométriques ; il additionne ensuite chacune des équations. Le tout définit un champ scalaire dont l’iso-valeur 0 est une surface lisse, représentant l’union des metaballs. Pour un modeleur, une metaball est donc… une primitive simple décrite par sa formulation implicite. Le mystère est donc levé ! Reste à nous pencher sur la chronologie des faits.

Naissance des premières metaballs

Au début des années 80, James Blinn, chercheur en infographie, souhaite animer une molécule d’ADN pour la série télévisée américaine de vulgarisation scientifique appelée Cosmos. Plus précisément, Blinn cherche à représenter les champs d’électrons évoluant autour des molécules : des objets en mouvement. Il écrit donc un algorithme faisant appel à la théorie des surfaces implicites et ses applications en géométrie et en physique. Blinn qualifie l’effet dynamique obtenu de blobby molecule sticking and unsticking [1]. Ces molécules « blobesques » constituent les premières metaballs connues. Toutefois le terme metaballs n’est pas de Blinn, mais d’une équipe de chercheurs japonais (Université de Osaka et Toyo Links) œuvrant au milieu des années 80 sur des algorithmes semblables. Au même moment en Nouvelle-Zélande et au Canada, les frères Wyvill travaillent également sur ce sujet, et qualifient leur résultat de soft objects [2]. Trois noms coexistent donc pour qualifier le même type d’objets géométriques.

Intégrant les résultats de ces travaux de recherche, les logiciels de modélisation 3D proposent alors des modules permettant de générer facilement des surfaces implicites : l’utilisateur n’a pas à écrire d’algorithmes, comme le faisaient Blinn, Mishimura et les Wyvill, mais peut entrer directement quelques paramètres pour voir son œuvre apparaître.

ZweiFische sous licence NY by CC 2.0

Reprenant l’expression de James Blinn, le logiciel de modélisation et d’animation The Advanced Visualizer commercialisé par Wavefront dans les années 80-90, baptise son module « BLOB », synthétisant ainsi l’acronyme Binary Large Object et l’aspect mou (blobby). Greg Lynn, l’un des premiers architectes ayant utilisé The Advanced Visualizer pour sa pratique, reconnaît avoir immédiatement apprécié cette fonctionnalité [3] : « At the level of geometry and mathematics, I was excited by the tool as it was great for making large-scale single surfaces out of many small components as well as adding detailed elements to larger areas. At a conceptual and technical level, I loved it and I do not expect this kind of nerdy involvement with the details of my profession to be shared or understood.«  [4]

Blender, logiciel de modélisation, d’animation et de rendu apparu à la fin des années 80, propose quant à lui un menu metaobjects pour créer deux types de surfaces implicites : en faisant varier une des valeurs x, y ou z autour d’un seuil, l’utilisateur peut générer une surface implicite ouverte (décrivant un plan) ou fermée (décrivant une surface gauche). Les metaballs sont au choix une ball, un tube, un plane, un ellipsoid, ou encore un cube. En outre, assimilé à une surface équipotentielle, chacun de ces objets est défini par un centre, une surface, une masse relative aux autres objets et un champ d’influence.

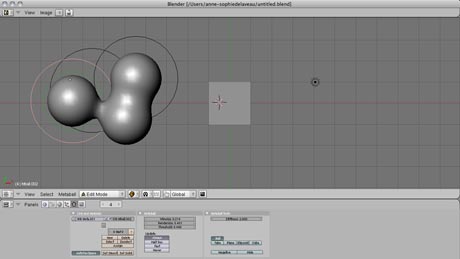
AS Delaveau sous licence NY by CC 2.0

Ces objets sont très facilement modifiables, comme l’écrit l’enseignant-chercheur Pascal Guitton : « En fusionnant plusieurs de ces surfaces élémentaires, on peut représenter des formes élastiques, des fluides, et surtout à les animer, ce qui explique leur grand succès parmi les infographistes. En effet, elles ont permis de lever certaines limitations des autres modèles pour décrire des objets de forme douce ou construits en accolant des formes élémentaires comme par exemple une main formée d’une paume et de cinq doigts, ce qui avec les approches précédentes entraîne des problèmes de raccordement géométrique de surfaces. » [5].

Les modeleurs baptisant différemment les modules gérant les surfaces implicites, blobs, metaballs, meta-clays et soft objects, ces noms seront couramment repris par les utilisateurs… entretenant ainsi la confusion entre technique d’infographie, interface du modeleur et forme molle !

Exemple architectural :

Korean Presbyterian Church (Queens, New York, 1995-99)

Les paragraphes suivants offrent une description du processus de conception qui nous semble fiable. Les traductions figurent en note de bas de page [6].

„Greg Lynn hat schon bei vielen Gelegenheiten erklärt, wie das Design für die Kirche entwickelt wurde. Wie im Computer verschiedene „meta blobs” entsprechend ihren einzelnen Zonen, denen Gravitationskräfte zugeordnet werden, interagieren. Wie sie wachsen and so lange miteinander zu neuen Formen verschmelzen, bis sich eine Art Aquilibrium eingestellt hat. Wie diese meta blobs für verschiedene Programme stehen, einzelne Räume symbolisieren, die sich zu einem großen Raum mit einer einzigen Oberfläche verbinden, der das gesamte Bauprogramm enthält. Wie sehr das auch die Bauherren liebten, weil sie tatsächlich selbst die Formen beeinflussen und die Dinge größer oder kleiner machen konnten, ohne die Kohärenz des Gesamtkonzeptes zu zerstören.“ (p. 71)

„In der ersten Phase des Designprozesses wurde eine Software ausgewählt, die es zuließ, verschiedene Teile des Raumprogramms, beispielsweise die verschiedenen Kapellen, den Altar und den Chorbereich, in „meta blobs“ zu lokalisieren, die dann zusammenwuchsen. Dann konnten ihre Größe und Beziehungen zueinander verändert werden, während sie verbunden blieben and das Gesamtdesign kohärent blieb.“ (p.  72)

Ces descriptions du processus de conception nous renseignent sur la manière dont les surfaces implicites ont permis à Greg Lynn de rendre compte du jeu entre relation et distinction des espaces constituant l’église. Il a ainsi modélisé séparément chacun de ces lieux – chapelles, autel, chœur, nef – différenciés par leur fonction, puis a fusionné les metaballs entre elles pour assurer l’unité générale. En outre, le recours aux surfaces implicites a permis de modifier facilement la taille de chacun de ces lieux, suivant les désirs des maîtres d’ouvrage.

Cet exemple n’est pas isolé dans la pratique de Greg Lynn, qui a d’ailleurs consacré un essai à ce type de modélisation [7]. Les surfaces implicites constituent en effet une réponse particulièrement pertinente et efficace à l’idée de « formes animées » que promeut l’architecte californien, c’est-à-dire des espaces complexes, différenciables et continus, multiples et singuliers, à l’opposé d’une vision traditionnelle et rigide de l’architecture « an inanimate, modular, divisible, universal and static body » [8]. Pour autant, Lynn n’oppose pas les surfaces implicites aux solides platoniciens : pour lui, il s’agit d’une même géométrie, dont la complexité correspond aux potentialités associées : « There is no essential difference between a more or less spherical formation and a blob. The sphere and its provisional symmetries are merely the index of a rather low level of interactions where the blob is an index of a high degree of information in the form of differentiation between components in time. […] Complexity, therefore, is not only always present as potential in even the most simple or primitive of forms; but, even more so, it is measured by the degree of both continuity and difference that are copresent at any moment. This measure of complexity (the index of which is continuity and differentiation) might best be described as the degree to which a system behaves as a blob » [9]. Les metaballs, parangons de l’architecture lynnienne?

Pour citer cet article

Anne-Sophie Delaveau, « M comme Metaballs », DNArchi, 25/0312012, <http://dnarchi.fr/culture/m-comme-metaballs/>

Bibliographie

Remerciements à Thierry Ciblac et à Julien Tierny pour l’éclairage géométrique et informatique !

Karen E.Goulekas, Visual Effects in a Digital World, Morgan Kaufmann,San Fransisco, 2001

Greg Lynn, Animate form, Princeton architectural press, New York, 1999

<http://interstices.info/surfaces>

<http://paulbourke.net/miscellaneous/implicitsurf/>

<http://www.awn.com/articles/reviews/science-visualization-and-educational-animation-siggraph-2001-next-big-deal>

<http://www.cs.otago.ac.nz/homepages/andrew/g2.pdf>