Auteur: Thierry Ciblac_
DOI : https://doi.org/10.48568/w6b2-da23

© Patrick Snels et Marina van der Lecq (source: http://www.snels-design.com/en/main/gallery/expanding_circle) superposé à un schéma Cabri effectué par Thierry Ciblac
Dans le domaine des outils informatiques destinés à l’enseignement de la géométrie, il existe une catégorie de logiciels dits de « géométrie dynamique » (Chamois, Cabri Géomètre, Geogebra…). Le terme « dynamique » doit se comprendre dans le sens où les figures construites ont la possibilité d’être animées en fonction des contraintes géométriques données lors de leur construction. Ainsi ce type de logiciel aborde-t-il les figures géométriques dans le plan au travers de leur logique de construction. Les points, droites, cercles etc. sont liés entre eux par les contraintes qui les lient (appartenance, parallélisme, perpendicularité, mesures…). Les figures ont donc la mémoire de l’enchaînement des constructions, ce qui permet leur adaptation à diverses configurations de manière interactive. Une conséquence induite de cette approche est par exemple que si l’on supprime un point servant de base à une construction, toute la construction en découlant sera supprimée. Une autre conséquence est qu’un point entièrement contraint (par exemple défini comme intersection de deux droites) ne peut pas être animé directement à la souris. Il ne peut changer de position que par l’animation des objets dont il découle. Ainsi, une figure ne peut être animée que par des éléments non entièrement contraints.
L’outil permet aussi l’évaluation des résultats, par exemple, l’alignement de points peut être vérifié, ou l’appartenance d’un point à un objet géométrique (droite, cercle, conique etc.). Une autre potentialité de cette approche est la possibilité de complexification ou de particularisation des constructions. Ainsi, par exemple, un point initialement libre dans le plan (c’est-à-dire pouvant être déplacé interactivement n’importe où dans le plan), peut être par la suite contraint à appartenir à une droite ou un cercle par exemple.
A titre d’exemple, nous montrons ici comment étudier la cinématique d’un mécanisme plan inspiré des sphères de Hoberman et développé par Patrick Snels et Marina van der Lecq :
© Patrick Snels et Marina van der Lecq (source: http://www.snels-design.com/en/main/gallery/expanding_circle)
Ce mécanisme est composé d’éléments identiques en forme de « boomerang » constitué d’un segment brisé en deux brins de même longueur. Ces éléments sont reliés à leurs extrémités et au niveau de la brisure par des articulations. Les sommets du mécanisme se déplacent sur des droites rayonnant à partir d’un centre. Sur la vidéo, le mécanisme est animé en faisant varier l’angle relatif de deux éléments connectés par une articulation, c’est pourquoi le centre n’apparaît pas fixe. Nous abordons le problème en supposant le centre fixe et cherchons l’angle entre les brins d’un élément.
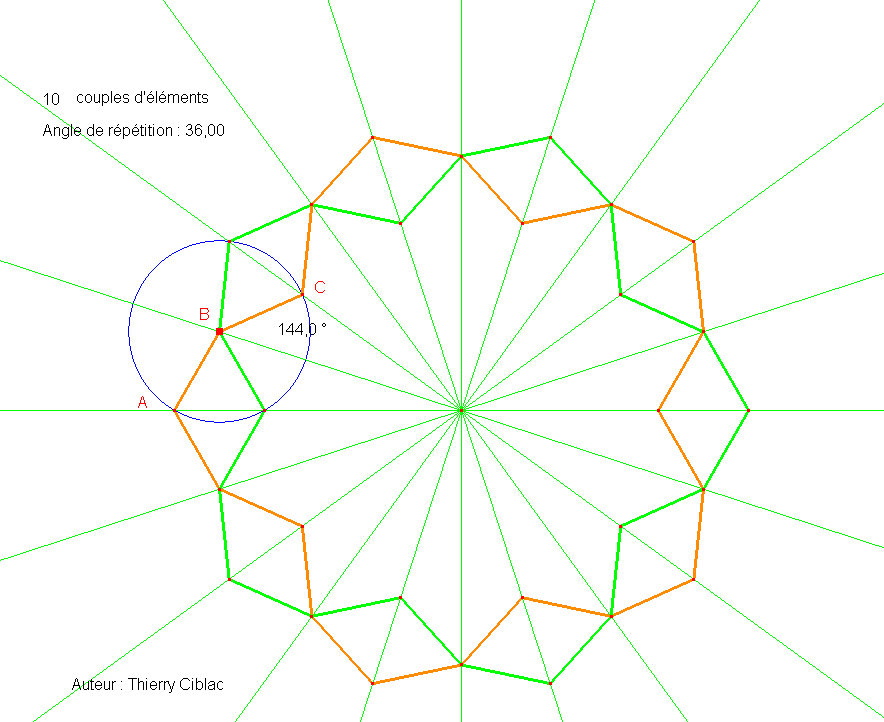
La forme de l’élément « boomerang » dépend du nombre de fois où l’on répète celui-ci pour former un mécanisme circulaire fermé. En assemblant dix couples de « boomerangs » articulés à leur brisure, les sommets (extrémités et brisure) se déplacent alors sur 20 rayons réguliers (tous les 18°). Prenons un élément boomerang. Notons A et C ses extrémités (voir figure ci-dessous) et B le points de brisure. Ces trois points sont contraints de se déplacer sur trois droites. Contraignons le point B sur un rayon, de tel manière qu’il ne puisse se déplacer que sur celui-ci. Les brins du « boomerang » ayant une même longueur L, on peut déduire le dessin de ce « boomerang » en cherchant ses extrémités A et C à l’intersection d’un cercle de rayon L avec les rayons adjacents.
Grâce à cette construction, on observe deux possibilités d’emplacement du « boomerang », donnant la position des éléments vert et orange reliés par une articulation en B. De plus, si on mesure l’angle entre les brins du boomerang, on peut observer que cet angle ne varie pas même si l’on fait varier la position de B sur le rayon. Un raisonnement sur les angles permettra au lecteur de confirmer rigoureusement cette observation empirique permise par le logiciel. Le mécanisme est ensuite complété par des symétries axiales par rapport aux rayons. La figure suivante, réalisée sur Cabri géomètre, illustre cet exemple. Pour animer la figure il faut bouger le point B avec la souris (installer auparavant le plugin en cliquant sur le lien au bas de la figure lors de la première utilisation).
POUR ANIMER LA FIGURE CLIQUER ICI
La géométrie dynamique, particulièrement simple d’usage, se révèle très puissante pour étudier des problèmes géométriques, mais aussi de cinématiques ou de représentation. Ainsi la géométrie descriptive et la perspective, combinées à l’usage de la géométrie dynamique, donnent-elles accès à l’animation des projections d’objets 3D à l’aide d’une seule construction…
Un grand merci à Rifat Nassif et Joaquim Silvestre pour m’avoir soumis ce problème, et à Patrick Snels et Marina van der Lecq pour avoir partagé leur travail!
Liens de sites de quelques logiciels de géométrie dynamique :
http://www.geogebra.org/cms/ (logiciel libre et gratuit)
Pour citer cet article
Thierry Ciblac, « Esquisses et géométrie dynamique », DNArchi, 28/03/2012, <http://dnarchi.fr/outils/esquisses-et-geometrie-dynamique/>